岡本　安晴（おやもと　やすはる） 日本女子大学名誉教授2020年04月23日

問題解決とか目標設定などにおいて、合理的判断を行うためには、データに基づいて関連情報を収集する必要がある。データ分析は、合理的客観的判断を支えるものである。データ分析における基礎的な考え方をPythonによるプログラミング例を示しながら具体的に説明する。

　Ａ国とＢ国でそれぞれ10人の男性をランダムに選び、表1のような身長のデータを得た場合の平均値と標準偏差(SD)を求める。

　前回は、「平均値に差がない」というモデル（帰無仮説）の下では、t値はt分布に従うということについて説明した。
 
　今回は、「平均値が異なる」としてt値の分布を求めてみる。例えば、A国の平均値が170、B国の平均値が180であるとする。標準偏差はともに6として、シミュレーション用のスクリプトを以下のように用意した。

muA = 170
muB = 180
sgm = 6
M = 10
 
N_Exp = 10000
t_values = []
for t in range(N_Exp):
　　X = scipy.stats.norm.rvs(loc = muA, scale = sgm, size = M)
　　Y = scipy.stats.norm.rvs(loc = muB, scale = sgm, size = M)
　　t, df = calc_t(X, Y)
　　t_values.append(t)
 
t_range = [v for v in np.arange(-4, 4, 0.25)]
p_values = [scipy.stats.t.pdf(t, 2 * M – 2) for t in t_range]
plt.hist(t_values, density = True)
plt.plot(t_range, p_values, linewidth = 3)
plt.plot([-5.45, -5.45], [0.0, 0.1], ‘r-o’, linewidth = 5, label = ‘t = -5.45’)
plt.legend()
plt.title(‘$\mu$A = {0} $\mu$B = {1}’.format(muA, muB), fontsize = 16)
plt.show()

 
　このスクリプトを実行すると、図４のグラフが得られる。

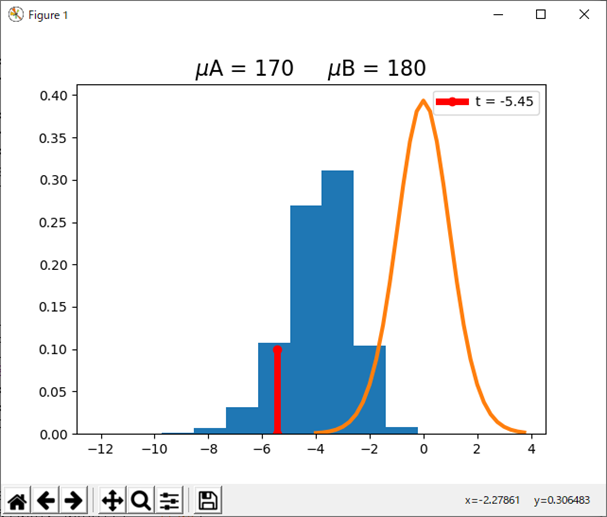
図４　平均値が170と180である場合のt値の分布
 
　平均値がmuA=170、muB=180と異なれば、t値の分布の中にt=-5.45は収まっている。
 
　どの程度のt値であれば、帰無仮説から予想される値からかけ離れていると判断するのか。帰無仮説の下では、t値の確率分布は図３（あるいは図４）に示されている曲線で表される。「平均値に差がない」という帰無仮説下ではt値は0に近い値をとると期待されるので、0からどれから離れているかが問題となる。分布の裾に左右に確率α⁄2の領域（棄却域と呼ぶ）をとり、この領域に入る値は0から十分に離れていると考える。左右の確率を合わせるとαになるので、帰無仮説が正しいときにt値が棄却域に入って誤って帰無仮説を棄却する確率はαである。この確率αを有意水準と呼び、α=0.05=5%と置くことが多い。
 
　自由度18のときの棄却域の境界値は、次のスクリプトで求められる。
 
df = 18
t_a2L = scipy.stats.t.ppf(0.025, df)
t_a2R = scipy.stats.t.ppf(0.975, df)
print(‘P(t<{0:.3f}) = 0.025, P(t>{1:.3f}) = 0.025′.format(t_a2L, t_a2R))
 
　実行すると次の出力を得る。
 
P(t<-2.101) = 0.025, P(t>2.101) = 0.025
 
　棄却域を図示するスクリプトは以下のようになる。
 
t_range = np.arange(-4.0, 4.0, 0.01)
p_values = scipy.stats.t.pdf(t_range, df)
plt.plot(t_range, p_values)
plt.hlines(0.0, -4.0, 4.0, color = ‘k’)
plt.vlines(t_a2L, 0.0, scipy.stats.t.pdf(t_a2L, df), color = ‘r’, linewidth = 2,
　　　　　label = ‘P(t<{0:<0.2f}) = 0.025'.format(t_a2L))
t_rangeL = np.arange(-4.0, t_a2L, 0.01)
plt.fill_between(t_rangeL, scipy.stats.t.pdf(t_rangeL, df), color = ‘r’, alpha = 0.5)
plt.vlines(t_a2R, 0.0, scipy.stats.t.pdf(t_a2R, df), color = ‘m’, linewidth = 2,
　　　　　label = ‘P(t>{0:<.2f}) = 0.025'.format(t_a2R))
t_rangeR = np.arange(t_a2R, 4.0, 0.01)
plt.fill_between(t_rangeR, scipy.stats.t.pdf(t_rangeR, df), color = ‘m’, alpha = 0.5)
plt.title(‘t distribution with df = 18’, fontsize = 16)
plt.legend()
plt.show()

 
実行すると図５のグラフを得る。

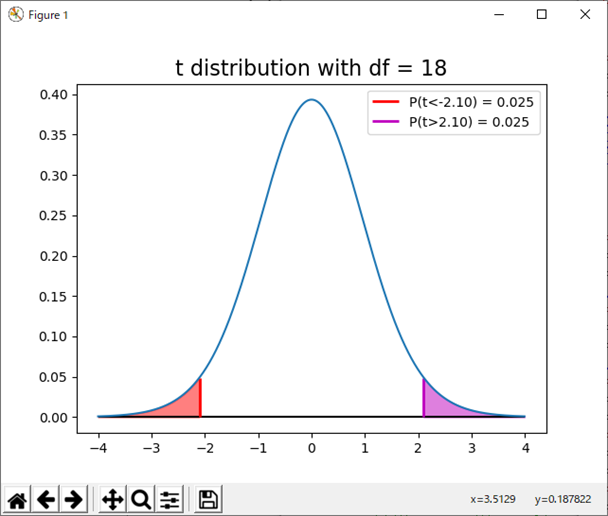
図５　棄却域
 
　左右の赤および赤紫色の領域が棄却域である。
 
　平均値に差があるのかないのかを問題にするときは、棄却域を分布の両側にとるが、平均値の差が正であるのか（あるいは負であるのか）が問題であるときは、分布の右の正の側（左の負の側）に確率αの棄却域を設定する。棄却域を分布の両側に取る場合を両側検定、片側にとる場合を片側検定という。
 
　表１のデータの場合、t値はt=-5.45で平均値に差があると判断されたが、t値はデータに応じていろいろな値をとる。いま、t値がt=-2.0であったとする。このときのt値の分布における位置を求めるため、次のスクリプトを用意した。
 
df = 18
t = -2.0
p = scipy.stats.t.cdf(t, df)
print(‘p = ‘, p)

 
　実行すると次の出力を得る。
 
p = 0.030410732834666266
 
　左から累積確率0.03に対応する位置である。有意素淳α=0.05のときは、左からα⁄2=0.025の位置に棄却域の境界が設定されるの、有意な差は認められない。しかし、有意水準をα=0.1=10%に設定するとα⁄2=0.05となり、左側の棄却域の境界α⁄2=0.05の累積確率に対応する値よりt値=-2.0は左側にあり、棄却域に入って有意差ありとなる。データから算出されたt値が棄却域に入るかどうかは、設定された有意水準αに依存して決まる。データから算出されたt値が棄却域に入る（帰無仮説が棄却される）最小の有意水準αをそのデータ（t値）のp値と呼ぶ（Conover, 1999）。
 

p値=帰無仮説が棄却される有意水準αの最小値

 
t値=-2.0の両側検定におけるp値は、p値=0.03×2=0.06=6%である。
 
　次回（第７回）は、最尤法について説明する。
 
 
 
引用文献

-Conover, W. J. (1999). Practical nonparametric statistics, 3rd edition. John Wiley & Sons, Inc.
-Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., & Rubin, D. B. (2014). Bayesian data analysis, 3rd edition. CRC Press.
-Martin, O. (2018). Bayesian analysis with Python, 2nd edition. Packt Publishing.
-岡本安晴（2009）．データ分析のための統計学入門。おうふう．
-ロベェッリ（栗原俊英訳、竹内薫監訳）（2017）．すごい物理学講義．河出書房新社．（原書：Carlo Rovelli (2014). La realtà non è come ci appare. Scienza E Idee）
　

連載一覧へ