連載
一覧Pythonで親しむデータ分析と確率モデル【第2回】―データの分布と確率モデル―

岡本 安晴(おやもと やすはる) 日本女子大学名誉教授
データに不確実性が伴うとき、そのモデル化に確率分布が用いられることがある。確率モデルとして、ベルヌーイ分布、二項分布、正規分布、カイ二乗分布、t分布、F分布、幾何分布、指数分布、ポアッソン分布、カテゴリカル分布、多項分布について、今回から複数回にわたって説明する。なお、本文中のスクリプトはプログラムの一部であることが多いが、プログラムの完全なスクリプトは筆者のウェブサイトに上げておいた。
ベルヌーイ分布
コイン投げの表が出るか裏が出るかのように、2つの事象の生起確率を表す分布である。事象を確率変数Xで表し、その2つの事象を数値の0および1で表しても一般性は失われない。例えばコイン投げのとき、表が出ればX=1とし、裏が出ればX=0とおく。確率変数Xに対する確率をP(X)で表し、2つの事象に対するそれぞれの生起確率を次のように設定する。
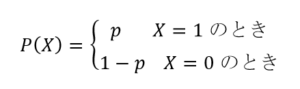
公正なコイン投げであれば、P(X=1)=p=0.5、P(X=0)=1-p=1-0.5=0.5と考えられるのでp=0.5とおけばよい。このベルヌーイ分布に従う確率変数Xの値は、モジュールscipy.statsのオブジェクトbernoulliのメソッドrvsにより得ることが出来る。メソッドを
scipy.stats.bernoulli.rvs(確率)
と呼び出せば、確率に設定された値をpの値とするベルヌーイ分布に従うXの値が返される。一般に、確率分布に従う値を返すメソッドの値は乱数(正確には疑似乱数)と呼ばれている。
公正なコイン投げを20回行う実験のシミュレーションとして、以下のスクリプトを書いてみた。
import scipy.stats
for i in range(20):
v = scipy.stats.bernoulli.rvs(0.5)
print(v, end = ”)
このスクリプトを実行すると以下の結果となる。
10101100111111010100
コイン投げのシミュレーションなので、例えば1は表、0は裏を表していると解釈する。乱数なので、特に初期値を設定しない限り、実行ごとに異なった結果を得る。再度実行すると
01011001001010001001
となった。
上のスクリプトの場合、メソッドbernoulli.rvsはベルヌーイ分布に従う乱数を1個返すだけであるが、2個以上をまとめて得ることもできる。パラメータsizeの値として個数を指定して
scipy.stats.bernoulli.rvs(確率, size=個数)
とメソッドを呼び出せば、指定した個数がNumpyでの配列型で返される。
次のスクリプトは、n_samples = 10個の乱数をまとめて得て、その10個の値とともにその総和(1の数)を出力するものである。
n_samples = 10
n_times = 5
for t in range(n_times):
v = scipy.stats.bernoulli.rvs(0.5, size = n_samples)
print(v, v.sum())
実行すると以下のような結果となる。角括弧[と]で囲まれたNumpyの配列型の値に続けて和(1の数)が出力されている。
[1 0 1 1 1 0 1 1 0 0] 6
[1 0 1 0 0 1 0 1 0 0] 4
[1 1 1 1 0 1 1 0 1 1] 8
[1 1 0 0 0 0 1 0 0 0] 3
[0 1 0 0 0 0 0 1 0 0] 2
上の例では、10個のベルヌーイ分布に従う事象の内、当該の事象、例えば1が何個あるかが示されている。一般に、N個のベルヌーイ分布に従う事象を1組として考え、その内で当該の事象、例えば表が何回あるかの個数を事象として扱うことがある。この確率分布が次に説明する二項分布である。
二項分布
独立なN個のベルヌーイ分布に従う事象において、注目した方の事象の個数の分布である。1つ1つのベルヌーイ分布に従う事象のサンプリングを試行と呼び、N回の試行をまとめて実験と呼ぶ。N試行からなる実験において当該の事象(X=1とする)の個数を表す確率変数をYとおくとき、その確率は次式で与えられる。
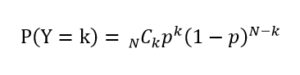
ここで、
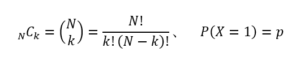
である。
各試行における確率がpである総試行数Nの二項分布に従う乱数は、モジュールscipy.statsのオブジェクトnormのメソッドrvsで得ることができる。メソッドを
scipy.stats.binom.rvs(総試行数, 確率)
と呼び出せばよい。例えば、次のスクリプトはN=10試行からなる二項分布に従う乱数を20個呼び出すものである。
p = 0.5
n_trials = 10
for t in range(20):
v = scipy.stats.binom.rvs(n_trials, p)
print(v, end = ‘ ‘)
実行すると以下のような結果を得る。
6 4 5 4 3 7 5 7 6 6 2 7 4 6 4 4 4 5 7 5
二項分布のメソッドをパラメータsizeを付けて
scipy.stats.binom.rvs(総試行数, 確率, size = 個数)
と呼び出すと指定した個数の乱数が返される。
次のスクリプトは、乱数をsize = 100000個生成してそのヒストグラムを描くものである。
data = scipy.stats.binom.rvs(n_trials, p, size = 100000)
x_range = [i – 0.5 for i in range(12)]
plt.hist(data, bins = x_range)
plt.show()
上のスクリプトを実行すると、図1のヒストグラムが表示される。
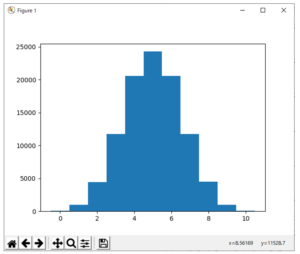
図1 二項分布のヒストグラム
図1は、試行数N=10の場合のグラフであるが、試行数を増やしてN=1000試行の場合を描くと図2に示すものとなる。
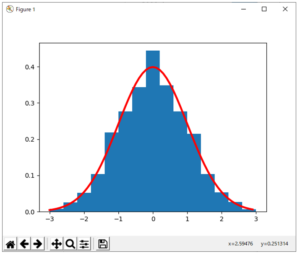
図2 試行数をN=1000試行に増やしたときのヒストグラム
ただし、二項分布の変数Yは、平均が0、標準偏差が1になるように標準化された値Zに変換されたものが横軸に用いられている。二項分布の確率変数Yの標準化変数Zは次式で与えられる。
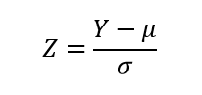
ここで、μとσは二項分布の平均と標準偏差で
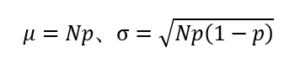
である。
二項分布はベルヌーイ分布に従う平均p、標準偏差![]() の確率変数の和と考えることができる。同じ分布に従う確率変数の和を標準化した確率変数の分布は、和をとるときの確率変数の数を増やしていくと標準正規分布と呼ばれる確率分布に近づくという性質がある(中心極限定理)。図2で示されている赤い曲線は、標準正規分布のグラフであるが、正規分布については次節で説明する。図2のグラフは以下のスクリプトによって描かれている。
の確率変数の和と考えることができる。同じ分布に従う確率変数の和を標準化した確率変数の分布は、和をとるときの確率変数の数を増やしていくと標準正規分布と呼ばれる確率分布に近づくという性質がある(中心極限定理)。図2で示されている赤い曲線は、標準正規分布のグラフであるが、正規分布については次節で説明する。図2のグラフは以下のスクリプトによって描かれている。
n_trials = 1000
raw_v = scipy.stats.binom.rvs(n_trials, p, size = 100000)
z_v = (raw_v – n_trials * p) / ((n_trials * p * (1 – p)) ** 0.5)
z_indx = [ v for v in np.arange(-3.0, 3.3, 0.4)]
plt.hist(z_v, bins = z_indx, density = True)
rng_x = np.arange(-3, 3, 0.1)
fv_norm = [scipy.stats.norm.pdf(x) for x in rng_x]
plt.plot(rng_x, fv_norm, color = ‘r’, linestyle = ‘-‘, linewidth = 3)
plt.show()
標準正規分布(standard normal distribution)の確率密度関数はscipy.statsのオブジェクトnormのメソッドpdfで与えられる。
正規分布
中心極限定理が示すように、多くの要因の効果が足し合わされて観測値が得られると考えられるときは、その観測値は正規分布に従うと説明されることがある。正規分布の確率密度関数ϕ(x|μ,σ)は次式で与えられる。
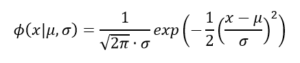
パラメータμは平均、σは標準偏差である。平均μ=0、標準偏差σ=1の正規分布は標準正規分布と呼ばれている。また、正規分布はガウス分布と呼ばれることもある。正規分布に従う乱数はscipy.statsのオブジェクトnormのメソッドrvsによって得ることができる。平均mu、標準偏差sigmaの正規分布に従う乱数をn個得るときは次のようにメソッドを呼び出せばよい。
scipy.stats.norm.rvs(mu, sigma, size = n)
平均と標準偏差のパラメータを省けば、標準正規乱数が生成される。パラメータsizeにタプルを設定すると対応する型のnumpy配列の形で生成された乱数が返される。
正規分布は誤差の分布に用いられることが多い。誤差はいろいろな要因によって生起すると考えられ、中心極限定理より正規分布で表されると説明される。誤差は正負両方の値を取り得るので足すとお互いに打ち消し合って小さい値になる。誤差の全体としての大きさは、2乗和で計算されることが多い。標準正規分布に従う独立な確率変数を5個用意し、その2乗和の分布を求めてみる。
次のスクリプトで、配列chi5には5個の標準正規分布の乱数の2乗和が10000設定される。
n = 10000
df = 5
z = scipy.stats.norm.rvs(size = (n, df))
z2 = z ** 2
chi5 = z2.sum(axis = 1)
この配列chi5に設定された10000個の値のヒストグラムを次のスクリプトで描いてみる。
plt.hist(chi5, bins = 30, density = True, label = ‘sum 5 squares’)
図3に示すヒストグラムが得られる。赤の曲線はカイ二乗分布と呼ばれる分布の確率密度関数のグラフである。同じ正規分布に従う独立な確率変数の2乗の和は、カイ二乗分布と呼ばれる分布に従う確率変数の定数倍になっている。
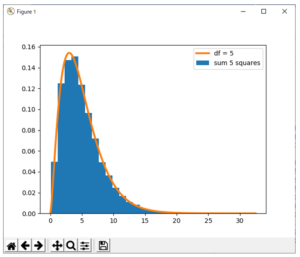
図3 正規乱数5個の2乗和とカイ二乗分布
カイ二乗分布の確率密度関数はscipy.statsのオブジェクトchi2のメソッドpdfで与えられる。カイ二乗分布の自由度と呼ばれているパラメータdfを指定して
scipy.stats.chi2.pdf(x, df)
と呼び出せば、xにおける確率密度関数の値が得られる。
図3におけるカイ二乗分布のグラフは次のスクリプトによって描いている。
max_x = chi5.max()
x2_values = np.arange(0.0, max_x, 0.1)
f_chi2_values = scipy.stats.chi2.pdf(x2_values, df)
plt.plot(x2_values, f_chi2_values, linewidth = 3, label = ‘df = 5’)
次節においてカイ二乗分布について説明する。
