連載
一覧Pythonで親しむデータ分析と確率モデル【第1回】―データ可視化からベイズ分析まで―

岡本 安晴(おやもと やすはる) 日本女子大学名誉教授
問題の解決とか目標の設定を合理的に行うためには、関連する情報を集めなければならない。このためにデータを収集することになる。いま、ある教師が新しく2つのクラスの授業を担当することになったとする。彼は、授業計画を立てるため、2つのクラスに学力を調べるテストを行ったところ表1のデータを得た。
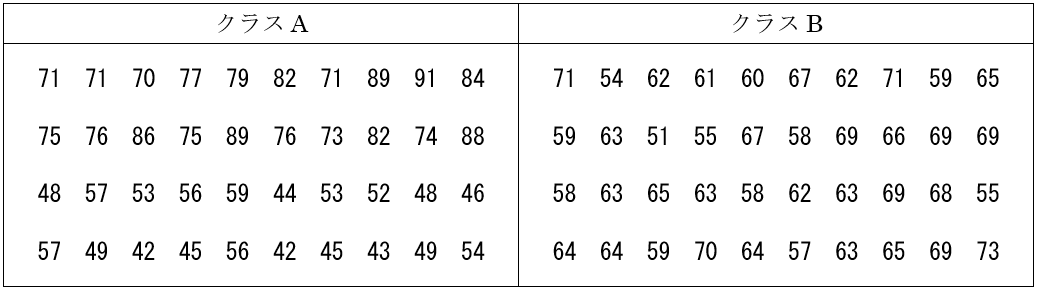
表1 2つのクラスの学力(仮想データ)
表1のように多くの数値があると、これらを眺めているだけでは比較が困難である。数値の集まりであるデータの分布の様子を表す統計量の1つに平均値がある。これは、データの総和をデータの個数で割ったもので、データの分布の中ほどの値を示す。これを求めるために、各クラスのデータをPythonのリストとして以下のように置く。
A = [71, 71, 70, 77, 79, 82, 71, 89, 91, 84,
75, 76, 86, 75, 89, 76, 73, 82, 74, 88,
48, 57, 53, 56, 59, 44, 53, 52, 48, 46,
57, 49, 42, 45, 56, 42, 45, 43, 49, 54]
B = [71, 54, 62, 61, 60, 67, 62, 71, 59, 65,
59, 63, 51, 55, 67, 58, 69, 66, 69, 69,
58, 63, 65, 63, 58, 62, 63, 69, 68, 55,
64, 64, 59, 70, 64, 57, 63, 65, 69, 73]
Pythonのインストールと使い方については、拙著<岡本安晴「いまさら聞けないPythonでデータ分析」丸善出版>の序章「Pythonの準備と使い方」で説明している。
AとBの平均値は次のスクリプトで計算できる。
mean_A = sum(A) / len(A)
mean_B = sum(B) / len(B)
算出された平均値は、次のスクリプトによって表示することができる。
print(‘Aの平均値 = ‘, mean_A)
print(‘Bの平均値 = ‘, mean_B)
上のスクリプトの実行結果は以下のようである。
Aの平均値 = 64.425
Bの平均値 = 63.25
平均点が64点と63点であるので、2つのクラスの学力は同じと考えてよいようである。クラスAとクラスBの授業は同じように行えばよいだろうという期待がもてる。しかし、それぞれのクラスの学力のヒストグラムを描くと、2つのクラスの学力の様子は全く異なることが分かる。ヒストグラムは次のスクリプトの実行で描くことができる。
plt.hist(A, alpha = 0.5, label = ‘Class A’)
plt.hist(B, alpha = 0.5, label = ‘Class B’)
plt.legend()
plt.show()
このスクリプトを実行すると、図1のヒストグラムが描かれる。
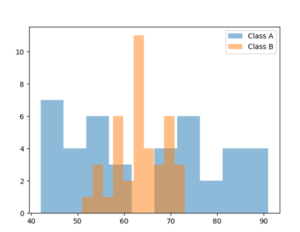
図1 クラスAとクラスBの学力
クラスBの生徒の学力は平均値を中心としてまとまっているが、クラスAは平均値より高いグループと低いグループに別れている。クラスBの授業は、平均値に合わせて行えばよい。しかしクラスAでは学力が2つに別れているグループのどちらに合わせて授業を行えばよいか、対応の難しいクラスである。
平均値の比較だけでは判断を間違うもう1つの例を取り上げる。就活をしているとして、2つの企業、企業Aと企業Bの年収をしらべたとする。企業の社員それぞれ1000人の年収を、Pythonのリスト変数に以下のように設定する。
A = [
572, 583, 1089, 381, 428, 354, 434, 554, 595, 392,
335, 444, 400, 388, 712, 485, 336, 386, 411, 523,
490, 584, 359, 505, 314, 339, 384, 737, 400, 557,
・
・
・
518, 324, 521, 529, 434, 366, 322, 333, 338, 900,
410, 600, 1050, 406, 572, 485, 468, 445, 487, 508
]
B = [
501, 507, 508, 501, 513, 487, 510, 495, 506, 498,
488, 495, 499, 501, 495, 497, 480, 500, 491, 508,
503, 510, 507, 500, 503, 503, 493, 492, 505, 501,
・
・
・
495, 490, 499, 493, 511, 506, 500, 494, 511, 494,
509, 491, 508, 518, 488, 493, 489, 494, 512, 494
]
各1000人分のデータを全て表記すると紙面を取り現実的ではないので省いた書き方をしているが、完全なスクリプトは筆者のウェブサイトに上げてあるので、そちらを参照して欲しい。
このデータに対して平均値を求め、出力するスクリプトを以下のように用意した。
a = np.array(A)
print(‘A社の平均 = ‘, a.mean())
b = np.array(B)
print(‘B社の平均 = ‘, b.mean())
このスクリプトの実行によって以下の出力を得る。
A社の平均 = 500.39
B社の平均 = 499.594
両者の平均年収はほぼ等しい。どちらの会社に入社してもよさそうである。しかし、両社の年収の分布を描いてみると異なった様相が浮かび上がってくる。分布の比較のためのスクリプトを以下のように用意した。
df = pd.DataFrame({‘Company’: [‘A’] * len(A) + [‘B’] * len(B),
‘Income’: A + B})
sb.stripplot(x = ‘Company’, y = ‘Income’, data = df, alpha = 0.5)
sb.violinplot(x = ‘Company’, y = ‘Income’, data = df, alpha = 0.5)
plt.show()
このスクリプトの実行で図2のグラフが描かれる。点(小円)が一人一人の年収の値である。バイオリンを立てたような図形は、年収のヒストグラムを横に90°回転して滑らかな曲線で表したもので横幅が頻度の推定密度を表している。
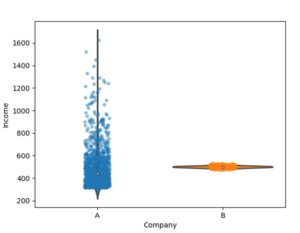
図2 A社とB社の社員の年収の分布
図2に示されている分布をみると、A社とB社の平均年収はほぼ同じであっても分布の示す内容は異なる。A社の場合、平均年収をかなり超える少数の社員がいるので、野心的な人はA社に入社して高収入を狙うことができる。しかし、多くの社員の年収は平均年収より少ない。これに対してB社は、社員の平均年収は全体の平均値のあたりにまとまっている。B社は、社員全員がほぼ同じ年収であるので、就職後の安心感がある。しかし、頑張ったから、あるいは会社に長年貢献したからといって年収が上がることは期待できない。A社を選ぶかB社を選ぶかは、仕事と生き方についての考え方で決まる問題である。
問題解決あるいは目標設定を客観的合理的に行うためには関連情報の収集が必要であり、データ分析はそのための基本的作業であるが、平均値を比較するだけでは状況の把握は不十分である。データの分布を視覚的に表すと、直感的理解が容易になる。グラフ描画は分析の基本である。拙著<岡本安晴「いまさら聞けないPythonでデータ分析」丸善出版>の第2章「グラフ描画」において、グラフ描画の解説を行っている。
次回(第2回)は、データ分布の数理モデルである確率分布について説明する。
なお、プログラム(Pythonスクリプト)の完全なリストは、筆者のウェブサイトに上げてあるので、そちらを参照されたい。
