川添　良幸（かわぞえ　よしゆき） 東北大学　未来科学技術共同研究センター2019年12月26日

　生まれてこの方、学習、経験によって常識は形成される。本質的に間違っていても生活には困らないため、実はとんでもない誤解をしていることもある。教科書問題は歴史だけではない。数学、理科、その他、何にでも沢山ある。
「将来の日本を担い、ノーベル賞受賞者となる若手研究者を育てるには、単なる改良型の教育・研究ではいけない」と言うのは川添良幸教授。科学の本質に迫るシリーズ連載。

第２回：電子は雲ではない

　２０１９年の５月２０日から国際単位系（SI, Système International d’unités）が原子単位に変わりました。とは言っても、急に変わった訳ではありません。１８７９年にフランスで決められた国際メートル原器が１００年も経つと１億分の１ほど伸び縮みしたため、１９６０年にクリプトンの出す橙色の波長に変更されたり、ｋｇ原器が１千万分の１ずれたりしました。人間の作った「基準」では、現在の技術が必要とする精度への対応に不十分なことが分かったのです。
 
　原子を基準とすればこういう問題は起きなくなります。こうして、より良い単位系を探した結果、７つの定数（セシウムの超微細遷移の振動数、真空における光速度、プランク定数、アボガドロ数、ボルツマン定数、電気素量、発光効率）を基本とした国際標準を決定することになったのです。すなわち今年から、長年親しんだ人間の尺度に合うMKSA単位系は廃止となり、原子が基本単位になりました。こうなると、量子力学は難しい、と匙を投げている訳には行きません。
 
　私にはとても懐かしい『ミクロの決死圏』という映画は１９６６年の作品ですが、物質のミクロ化に成功した科学者が脳出血を起こし、彼を助けようと医師団がその体内に小さくなって入って行って救命するというストーリーでした。今では現実となったレーザー縫合術等も登場して当時良くこんなことまで考えたものだと思います。
 
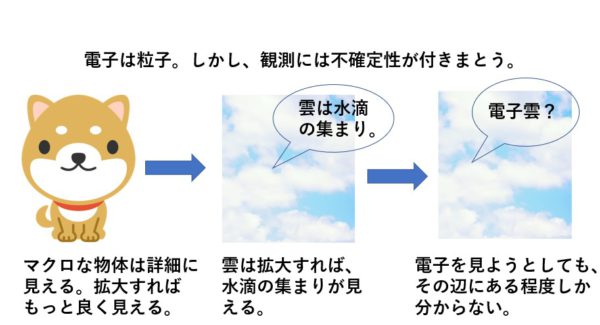
　しかし、ミクロとは言っても量子力学が対象とするサイズに比べれば遙かに大きく、「拡大すればよく見える」範囲です（映画としてちゃんと映っています！）。我々が見ている「もの」と量子力学の取り扱う対象物の違いは、量子系はいくら精度を上げても、「ちゃんとは見えない」ことなのです。電子を精度良く見ようとして光を当てても、位置と運動量は同時には確定出来ません。ピンぼけ写真しか撮れないのです。これを不確定性原理と呼んでいます。
 
　電子は素粒子物理学では、軽い粒子（レプトン）の一種に分類されます。量子力学のシュレディンガー方程式中でも、その位置と質量が現れます。しかし、マクロな「もの」と違い、その位置と運動量は同時に観測出来ないのです。この「その辺にある」範囲を電子雲と呼びます。電子が雲な訳ではなく、およそその辺にはあるという観測しか出来ないので、その範囲を雲と呼ぶのです。

 
　最近は１電子を扱い、電流を基盤とする従来の情報処理を桁違いに高速化・高容量化するスピントロニクスが喧伝されます。電子のスピンと言うのですが、位置と運動量さえ同時に特定出来ない電子の回転が見える訳ではありません。磁場の中を電子が移動すると２つの方向に分かれるという実験事実を説明するためにスピンの概念が生み出されました。目に見えない電子をたとえ話で理解しようとするのには限度があります。
 
　原子に関係するもう一つの話題として、今年は元素の周期律表が発表されてから１５０年の節目に当たります。
 
　メンデレーエフの名前は科学者は当然全員知っていますが、一般的にそんなに知られている訳ではありません。ところが、ロシアでは誰でも知っているのです。その理由は、もちろん周期律表ではなく、彼がウオッカのアルコール度の４０％を決めた人だからです。それより濃くても薄くても胃まで直行しません。１５０年前にメンデレーエフは多くの人を対象にして胃まで直接届く（感じる）アルコール度を決定したのです。ロシアでは体を温める必要からこの４０％が大事なのです。日本やヨーロッパの温暖な気候ではそんなに高いアルコールではなく１５％位のが好まれます。所変われば品変わるの良い例です。
 
　閑話休題。実は、古典力学も量子力学と同様に難しいのです。今の学校教育では、重力下でのボールの運動等のレベルだけを教え、複雑なコマの歳差運動や相対性理論はほぼ教えずに、何と量子力学を始めます。特殊相対論を習っていれば、観測の問題が重要なことをはっきり理解出来ます。コマの運動を確実に理解していれば、電子のスピンも良く分かるのです。そのためには球座標とラグランジアンを勉強しなければなりません。また、ハミルトニアンは、位置の時間での２次微分の一つの式であるニュートン方程式を、位置と運動量を別々に扱い、２つの１次微分方程式に書き換えたものです。この定式化は解析力学と呼ばれますが、位置と運動量を別々に扱えることから不確定性原理の表現が可能です。
 
　単にシュレディンガー方程式を解いていても何も分かりません。それどころか、最近では欧米で開発されたソフトウェアを使ってシミュレーション計算をし、「理論」の論文を書く人ばかりになってしまいました。嘆かわしいことです。もっと基礎教育を充実させなければ、新しい原子・分子の時代に正しく対応し、さらに先の理論を生み出せる人材は育ちません。
 
 
 
参考文献

「磁化の発現と高飽和磁化の可能性」、川添良幸、磁性材料活用辞典、藤崎敬介編著、コロナ社、2018年

連載一覧へ