連載
一覧Pythonで親しむデータ分析と確率モデル【第3回】―データの分布と確率モデル―

岡本 安晴(おやもと やすはる) 日本女子大学名誉教授
データに不確実性が伴うとき、そのモデル化に確率分布が用いられることがある。確率モデルとして、ベルヌーイ分布、二項分布、正規分布、カイ二乗分布、t分布、F分布、幾何分布、指数分布、ポアッソン分布、カテゴリカル分布、多項分布等、様々なものが挙げられる。前回に続き、各モデルの概要を説明する。なお、本文中のスクリプトはプログラムの一部であることが多いが、プログラムの完全なスクリプトは筆者のウェブサイトに上げておいた。
カイ二乗分布
標準正規分布に従う独立なN個の確率変数の2乗和は自由度df=Nのカイ二乗分布に従う。自由度df=νのカイ二乗分布の確率密度関数χ_ν^2 (x)は次式で与えられる。
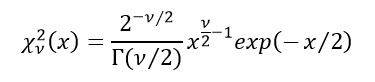
統計的検定では、平均値の差とその標準偏差(標準誤差)との比が統計量として使われることがある。「平均値の差が0である」という仮説(帰無仮説と呼ばれる)の下では、分子は平均が0の正規分布となる。分母は、誤差が正規分布であるという仮定の下では、カイ二乗分布を自由度で割った値の平方根という形をとる。
標準正規分布に従う乱数と、自由度3のカイ二乗分布に従う乱数を自由度3で割った値の平方根との比の値のヒストグラムを描いてみる。
標準正規分布に従う100000個の乱数は次のスクリプトによって得ることができる。
n = 100000
z = scipy.stats.norm.rvs(size = n)
自由度3のカイ二乗分布に従う100000個の乱数を自由度で割ったものの平方根は次のスクリプトによって得ることができる。
df = 3
ch2 = ((scipy.stats.chi2.rvs(df, size = n)) / df) ** 0.5
オブジェクトchi2のメソッドrvsは、自由度dfのカイ二乗分布に従う乱数をn個生成するものである。
これらの乱数の比は、次のスクリプトで求めることができる。
t_v = z / ch2
ヒストグラムを次のスクリプトで描くと図1のヒストグラムが描かれる。
plt.hist(t_v, bins = t_range, density = True, label = ‘z/$\chi$’)
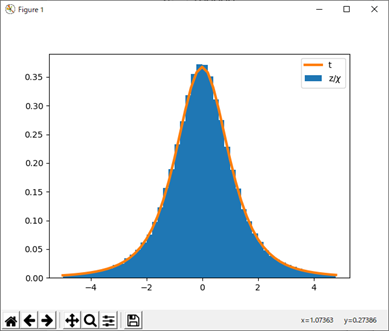
図1 正規分布とカイ二乗分布の平方根との比とt分布
図中の赤い曲線はt分布のグラフである。t分布の確率密度関数はscipy.statsのオブジェクトのメソッドpdfとして用意されている。以下のスクリプトでt分布の確率密度関数が描かれている。
t_range = np.arange(-5, 5, 0.2)
t_dv = scipy.stats.t.pdf(t_range, df)
plt.plot(t_range, t_dv, linewidth = 3, label = ‘t’)
t分布
標準正規分布に従う確率変数とカイ二乗分布に従う確率変数を自由度νで割ったものの平方根との比は、自由度νのt分布に従う。自由度νのt分布の確率密度関数は、次式で与えられる。
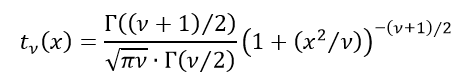
自由度νのt分布に従う乱数は、scipy.statsのオブジェクトtのメソッドrvsによって得ることができる。次のコードにより、指定された自由度の乱数がsizeに設定された個数生成される
scipy.stats.t.rvs(自由度, size = 個数)
パラメータsizeを省くと、1個生成される。
次のスクリプトは、自由度5のt分布に従う乱数を10生成して表示するものである。
samples = scipy.stats.t.rvs(5, size = 10)
print(samples)
実行すると、以下のように出力される。
[ 0.37758867 1.82906635 0.98691856 -0.15739102 0.10314699 0.38749395
-0.4969515 1.26766942 -2.26486131 -0.63051386]
t分布の確率密度関数は、scipy.statsのオブジェクトtのメソッドpdfで与えられる。次のコードで、指定した自由度の確率密度関数のxにおける値が得られる。
scipy.stats.t.pdf(x, 自由度)
自由度が1,2,10のt分布の確率密度関数と標準正規分布の確率密度関数のグラフを描くスクリプトを以下のように用意した。
x_range = np.arange(-4.0, 4.0, 0.1)
f_t1 = scipy.stats.t.pdf(x_range, 1)
f_t2 = scipy.stats.t.pdf(x_range, 2)
f_t10 = scipy.stats.t.pdf(x_range, 10)
f_n = scipy.stats.norm.pdf(x_range)
plt.plot(x_range, f_t1, label = ‘df = 1’)
plt.plot(x_range, f_t2, label = ‘df = 2’)
plt.plot(x_range, f_t10, label = ‘df = 10’)
plt.plot(x_range, f_n, label = ‘normal’)
plt.legend()
plt.show()
このスクリプトを実行すると、図2のグラフが描かれる。t分布の自由度が大きくなると正規分布に近づくことがわかる。
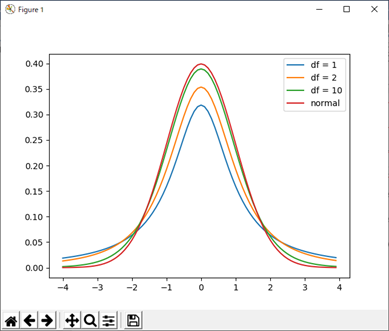
図2 t分布と正規分布
正規分布と自由度で割ったカイ二乗分布の平方根との比はt分布に従う確率変数になるが、自由度で割ったカイ二乗分布同士の比はF分布という確率分布に従う。次節においてF分布について説明する。
F分布
誤差などは正規分布すると仮定されることが多い。また、誤差の大きさはその2乗和で評価されるので、これはカイ二乗分布の定数倍となる。誤差(あるいは残差)の大きさの比較においてカイ二乗分布を自由度で割ったものの比が統計量として用いられることになる。
次のスクリプトは、自由度3のカイ二乗分布に従う乱数をその自由度で割ったものと自由度5のカイ二乗分布に従う乱数をその自由度で割ったものの比を求めヒストグラムを描くものである。
n = 100000
df1 = 3
ch2_1 = (scipy.stats.chi2.rvs(df1, size = n)) / df1
df2 = 5
ch2_2 = (scipy.stats.chi2.rvs(df2, size = n)) / df2
F_v = ch2_1 / ch2_2
F_range = np.arange(0.0, 20.0, 0.25)
plt.hist(F_v, bins = F_range, density = True)
上のスクリプトを実行すると、図3のグラフが描かれる。図中、赤い曲線はF分布のグラフである。自由度ν_1のカイ二乗分布に従う乱数を自由度ν_1で割ったものと自由度ν_2のカイ二乗分布に従う乱数を自由度ν_2で割ったものとの比は自由度(ν_1,ν_2 )のF分布に従い、その確率密度関数は次式で与えられる。
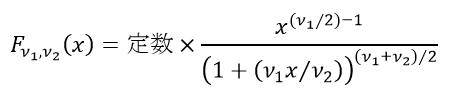
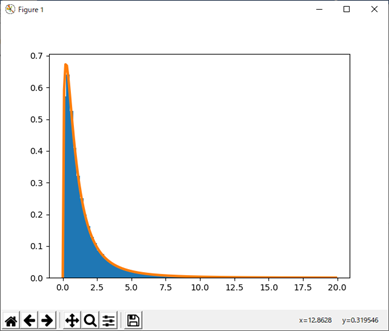
図3 カイ二乗分布を自由度で割ったものの比とF分布
F分布の確率密度関数の値は、scipy.statsのオブジェクトfのメソッドpdfによって得ることができる。自由度(df1, df2)のF分布のxにおける確率密度関数の値は、次のコードで得ることができる。
scipy.stats.f.pdf(F_p, df1, df2)
図3の赤い曲線は次のスクリプトで描かれている。
F_p = np.arange(1.0e-300, 20.0, 0.1)
F_dv = scipy.stats.f.pdf(F_p, df1, df2)
plt.plot(F_p, F_dv, linewidth = 3)
次回では、ある時間内におけるウェブサイトへのアクセス数とか、事象の生起を数えるときの確率モデルについて考える。
